INP8084118 - MATHEMATICAL PHYSICS 2022-2023
Schema della sezione
-
-- Monday 10:30 - 12:15 EF5 (Ex Fiat)
-- Wednesday 10:30 - 12:15 EF5 (Ex Fiat)
-- Thursday 8:30 - 10:15 EF5 (Ex Fiat)
-
-
Two examples from population dynamics: Malthusian and Verhulst growth models and their explicit solutions. Phase-portrait of Malthusian and Verhulst models, discussion of equilibria’s role. Other two examples of 1-dim vector fields (explicit and qualitative study). Some recalls on vector fields: Cauchy problem, Cauchy existence and uniqueness Theorem, one example of a C^0 vector field without uniqueness of solutions. Video of Lecture 1:
Access key: 0c@=T@0q
(or see Media Gallery)
-
-
-
Fundamental definitions for vector fields: flow, orbit, phase-space, phase-portrait, equilibrium. Properties of flows and orbits. Example of 2-dim vector fields and related phase portraits. Phase portraits (by using explicit solutions) of the harmonic oscillator, the gravitational vector field, the free particle, the harmonic repeller. Qualitative discussion of "stability", "instability", "asymptotic stability”. Some exercises on 1-dim and 2-dim vector fields. Video of Lecture 2:
https://unipd.zoom.us/rec/share/JtfQ54Nlzc3MKl0Z7w7iqZph3TWnor8UN88AVF8tMOkqOcGMYmYxPgF6vvbWZvb0.ABQlEGbs8guspwmq
Access key: sV1y1.fJ
(or see Media Gallery)
-
-
Double Pendulum - "Home Experiment":
Double Pendulum - "Computer Simulation":
Magnetic Pendulum - "Home Experiment":
3 Magnets Pendulum - "Basin of Attraction":
Weather and Chaos: The Work of Edward N. Lorenz:
-
The Allee affect, also with a "constant hunting" parameter. Dependence on initial data. General theorem about the exponential convergence-divergence of trajectories. Dependence on initial data in the previous examples: Malthusian model, x’ = 1, the harmonic oscillator, the harmonic repeller. General observations about sensitivity to initial conditions: the magnetic pendulum, the double pendulum. From determinism to chaos... Vector fields depending on parameters. Bifurcations and bifurcation diagrams. First exercises of vector fields depending on a real parameter. Video of Lecture 3:
https://unipd.zoom.us/rec/share/7j3EUG4vVm0E5k4X_ntN1q1xbXWc_ypnlInZ-uT4TqYSxx0ssxQUdLzgt_lTf-nD.DVmQ8Y4WBNzb-3Yq
Access key: gWi#2fr$
(or see Media Gallery)
-
-
-
5 exercises of 1-dim vector fields depending on a real parameter and their corresponding bifurcation diagrams. Remarks about the role of X'(x) for the quality of equilibria in the 1-dim case. Linearization of a vector field (examples in 1-dim, 2-dim, 3-dim). Video of Lecture 4:
Key access: Y*zs0i!A
(or see Media Gallery)
-
-
-
Linearization of second order differential equations, example: simple pendulum with friction (equilibria and linearization around equilibria). n-dim linear vector fields: the matrix exponential. 3 exercises on the matrix exponential. 1 exercise: global solution of a 2-dim linear vector field, remarks on the role of eigenvectors and eigenvalues. Video of Lecture 5:
https://unipd.zoom.us/rec/share/kp7E-YnfEHj5m4TQtK3xXgOJ2V8S4mlNTdVbTq5Fmyg5V_5GikorPq2zN3vyV7GL.R3Y6d9EgKa6mzr6c
Key access: 7x6*ir7w
(or see Media Gallery)
-
-
-
Classification of 2-dim linear vector fields, with the matrix A diagonalizable: node, saddle, star node, center, spiral. 1 exercise. Bifurcation diagram for 2-dim linear vector fields, with A diagonalizable. Video of Lecture 6:
https://unipd.zoom.us/rec/share/a1e6hdtHl8aKLIosTfElMzMpO0G2C-XJOdBir-FIef6MQcb2TAVuIj9ju0GWlGM.0W0s1E9LmmgvfF-xKey access: z4&UL+op
(or see Media Gallery)
-
-
-
6 exercises on: bifurcation diagrams, linear systems, the effect of nonlinear terms. Hyperbolic and elliptic equilibria: definitions. Video of Lecture 7:
https://unipd.zoom.us/rec/share/8fs9slRz5XhbjPgXpUYXUJX8D1aKMjPD54zuC7g77mlBccUTJff36KqTiYZQ4H5L.b2oxoy1fJIqtukAk
Key access: aF%tm^k2
(or see Media Gallery)
-
-
-
Grobman-Hartman Theorem and First Lyapunov Theorem: only statements. Topologically stable, unstable and asymptotically stable equilibria: definitions and discussion. Lie derivative. C^0 and C^1 version of Lyapunov Theorem for stability with proof. Video of Lecture 8:
https://unipd.zoom.us/rec/share/m4D4wcqSvSr9caehoFmZIYeg1R_lKrPnKiXBglCsKaguyWYlIPRKw1aRcgP0IWaR.eUIcTI461fV5orYY
Key access: 5qV=3#jJ
(or see Media Gallery)
-
-
-
Lyapunov Theorem for asymptotic stability with proof. The harmonic oscillator with friction: asymptotic stability of (0,0) by an appropriate Lyapunov function and by the spectral method (first Lyapunov method). A model for rabbits and sheep: the principle of competitive exclusion. 1 exercise on stability. Video of Lecture 9 (first and second part):
https://unipd.zoom.us/rec/share/Kje2H987FCO7OCkexiHLlMPee9uufYZpi6a17puFKHxRib1U0TvydiGCvGQgiSIl.uZoXe8S_XTNQWEHL
https://unipd.zoom.us/rec/share/qE-EBgPd9tKbBo4cRrVcVJa5kGfxaBKqBi7SXDrOnBqJt-kQM7IcwKJK11mdFif5.w2ir5UW9eIR1ID2G
Access key: wh1YM.5# -- 8CVaB*0! (respectively)
(or see Media Gallery)
-
-
-
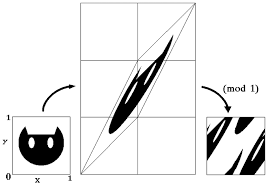
3 exercises on Lyapunov functions, spectral method (the pendulum with friction), bifurcation diagram. Phase-portraits of 1-dim conservative systems: general properties. The phase-portrait (by using the conservation of energy) for the harmonic oscillator and the harmonic repeller. The Arnold's cat map (hints).
Video of Lecture 10:
Key access: cNh.XZL1
(or see Media Gallery)
-
-
-
The phase-portrait (by using the conservation of energy) for the gravitational force near earth, the Keplerian gravitational force, the pendulum. Phase-portrait of the pendulum, also here (until 2:54):
3 exercises on phase portraits for second order conservative systems, included the period of a closed trajectory. Video of Lecture 11:Key access: WrD$30&9
(or see Media Gallery)
-
-
-
Self-evaluation questions and exercises.
-
5 exercises on phase portraits of first order systems, second order conservative systems, equilibria and their quality, bifurcations, first integrals and Lyapunov methods... Attractiveness is impossible in conservative systems, with proof. Video of Lecture 12:
https://unipd.zoom.us/rec/share/18Ve-Ni_6goSj3TcZh4_n2vxcQMZg6vMrGyDQGmGtaZ5u-Z6sDxctlmLjFF14tIK.oqovzjGK5tMu6Fc6Key access: nd$hG7f+
(or see Media Gallery)
-
-
-
Two Lotka-Volterra (prey-predator) models: phase-portraits and discussion. The limit cycle phenomenon: definition, a first simple example, limit cycles are not possible in linear systems (with proof). A model for the mechanical clock: from flows to discrete dynamics...
Video of Lecture 13 (first and second part):
https://unipd.zoom.us/rec/share/3r2DyoD1JwcPen_MSCOZvNE-ipfc2mEJ9TKIPfFNkRjoqsroeyPZ_h0YpZ1HfMLY.KOgwfybsFGTlN3yW
https://unipd.zoom.us/rec/share/ddyLIMy1ig64DS4CvG8Ss33YyNAuDskqqW6OTanahnHVOwtSvCamcmXlEsJsYYiq.bzayv02e4BMYWnZa
Access key: anz06B+% -- G*9a2JjZ (respectively)
(or see Media Gallery)
-
-
-
Discussion on mechanical clock and swing. Discussion on "more realistic" Lotka-Volterra models. Ready to appreciate and understand the whole video:
One dimensional maps: fixed points linearly (un)stable, the cobweb plot. The map f(x) = x^2, the logistic map: bifurcation diagrams.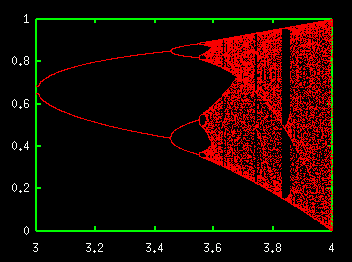
1 exercise on a nonlinear vector field in the plane. Video of Lecture 14:
https://unipd.zoom.us/rec/share/4C0gTVIxEz-x5TP-Vv_gBKzZRgL3yFP71Q_lU5KjLoqUWOSYbOhWFUVle8GgaEIY.WR_BZeeEplHi9v0tKey access: 39Zgx#As
(or see Media Gallery)
-
-
-
2 exercise on 1-dim conservative dynamical systems: phase-portraits, quality of equilibria, estimate of periods. In the pendulum, the time to reach the unstable position is +infinity (explicit computation). Constraints: local parameterizations of a surface and a curve. Examples: sphere, circle. Video of Lecture 15 (ONLY UNTIL 1:28):
https://unipd.zoom.us/rec/share/gVBvli7EFfzujTrDy7dYvecFOBowx2u_pbUKCohcaM8ELmHBOf9ugLsuWWsAfgTZ.MuiVrIJBXaf-4RLSKey access: gL.D3QC.
(or see Media Gallery)
-
-
-
Explicit computation of constraint forces for a fixed point on a table, a point in uniform circular motion on a table, the pendulum. Ideal constraints: definition and discussion. Newton's equations of a constrained dynamical systems. The formula for the kinetic energy of a constrained dynamical systems of N points. Video of Lecture 16:
Key access: #9$z$N1e
(or see Media Gallery)
-
-
-
Proof of the formula for the kinetic energy for a system of points in terms of Lagrangian coordinates. The matrix of the kinetic energy is symmetric and positive definite (with proof). Various examples: kinetic energy for a point in polar and spherical coordinates, the pendulum, the double pendulum and other constrained systems. Lagrangian components of forces (definition), the conservative case. Lagrange equations in the general and in the conservative case (formula and discussion, the detailed proof will be done the next Monday). Video of Lecture 17:
Key access: G^+x5s&i
(or see Media Gallery)
Joseph-Louis Lagrange - Mécanique analytique (1788) - page 39
-
-
-
G. Benettin talk: The uncertain path of determinism in Classical Mechanics.
-
-
-
3 exercises on the first half part of the course (in preparation to the first partial written exam of tomorrow). Video of Lecture 19:
https://unipd.zoom.us/rec/share/J3D3Yx368yhGxuP-GhoQcqccXHP7gFeahAX5nOkWQ0ju-N8HGI06Y1IR5o3rQYX8.VBYNF2ithscHp5UA
Key access: ^nxF93&H
(or see Media Gallery)
-
-
-
3 exercises on Lagrangian formalism: Lagrangian (with gravitational, elastic, centrifugal potentials), equilibria, their stability, first integrals. Detailed proof of Lagrange equations, the Jacobi integral (with proof). Video of Lecture 20:
Key access: eq=i=336
(or see Media Gallery)
-
-
-
2 exercises on Lagrangian formalism: Lagrangian (with gravitational, elastic, centrifugal potentials), equilibria, their stability, first integrals. Normal form of Lagrange equations for mechanical Lagrangians (with detailed proof). Cyclic coordinate (definition). Equilibria and stability for mechanical Lagrangians (if q* is a strict local minimum of the potential energy then (q*,0) is a stable equilibrium, with proof). Video of lecture 21:
Key access: nWZg=&P3
(or see Media Gallery)
-
-
-
1 exercise on Lagrangian formalism. Rigid motion (definition). Complete proofs of Poisson formula and fundamental formula of rigid motions. Lagrange-Dirichlet theorem (only statement, the proof will be given during the next lecture). Video of lecture 22:
Key access: 6=N2C%DL
(or see Media Gallery)
-
-
-
Complete proofs of Lagrange-Dirichlet theorem, Konig theorem. Inertia matrices for the bar, the ring, the disc, the rectangle (the square). 2 exercises on Lagrangian formalism. Video of lecture 23:
Key access: ePZgBZ8!
(or see Media Gallery)
-
-
-
2 exercises on Lagrangian formalism. A partial inversion of Lagrange-Dirichlet theorem: the non-degenerate Hessian theorem (only statement). Routh method: the formula for the reduced Lagrangian (proof will be give tomorrow). Video of lecture 23:
Key access: 2$#4n+oF
(or see Media Gallery)
-
-
-
Routh method: complete proof of the formula for the reduced Lagrangian. Reduced Lagrangian and motions for a conservative central force on the plane. Geodesics on the torus (phase-portrait for the reduced Lagrangian, re-construction of motions), 1 exercise on Lagrangian formalism.
Video of lecture 25:
Key access: MXT.Q@7l
(or see Media Gallery)
-
-
-
Small oscillations around a stable equilibrium of a mechanical system: complete discussion included formula for the characteristic frequencies. 2 exercises on Lagrangian formalism. Video of lecture 26:
Key access: GzFN2#uD
(or see Media Gallery)
-
-
-
Potential depending on velocities: the explicit formula for the generalized potential for the Coriolis force and the Lorentz force. Exercises on Lagrangian formalism (Lagrangian, equation of motions, equilibria, stability, reduced Lagrangian, study of the reduced system...). Video of lecture 27:
Key access: 44yC%Ln$
(or see Media Gallery)
-
-
-
Complete introduction, discussion and proof of Noether theorem. The case of a central potential: the total quantity of motion and the total angular momentum are conserved. Exercises on Lagrangian formalism.
-
-
-
Chaos in "simple" dynamical systems: the standard map and the Frenkel-Kontorova model.
The Van der Pol equation, existence of the limite cycle for (very) large and (very) small values of the parameter. 1 exercise on Lagrangian formalism. Video of lecture 29:
Key Access : 7pE!4TmX
(or see Media Gallery)
-
-
-
The spherical pendulum: reduction to a 1-dim conservative system, its equilibrium and stability; re-construction of the dynamics for the original system.
Linearized equations of the spherical pendulum near the south pole (stable equilibrium). The magnetic stabilization (as an application of generalized potentials). Video of lecture 30:
Key Access: rs3%N*6Q
(or see Media Gallery)
-
-
-
Foucault pendulum: notes for a linearized system.
1 exercises on Lagrangian formalism. Video of lecture 31:
Key Access: 0kbN3!Cm
(or see Media Gallery)
-
-
-
Functionals, examples, the Action functional. Space of curves, space of loops. Gateaux derivative of a functional at a given curve. The Principle of Least Action, complete proof. Remarks on the Principle of Least Action, determinism vs finalism. Video of lecture 32:
Key Access: *aS0$6R=
(or see Media Gallery)
-
-
-
Free motions and geodesics, the corresponding variational problems. Free motions are geodesics, with detailed proof. Geodesics are free motions, only discussion of the result. Geodesics on the plane and on the sphere. The function on the plane giving a revolution surface with minimal area is the catenary. Application to soap films. 1 exercise on the reduced Lagrangian.
Video of lecture 33:Key Access: 90XB.SC=
(or see Media Gallery)
-
-
-
The Legendre transform: definition and proof that it is a local diffeomorphism. The Legendre transform is a global diffeomorphism in the mechanical case. The Hamiltonian, Hamilton equations, the symplectic matrix. The Legendre transform conjugates (i.e. sends solutions into solutions) Lagrange and Hamilton equations, with proof. 1 exercise on Lagrangian mechanics. Video of lecture 34:
Key Access: &we@8$M8
(or see Media Gallery)
-
-
-
F. Cardin talk: Tullio Levi-Civita and the Parallel Transport Theory
-
-
-
Exercises. Video of lecture 36:
https://unipd.zoom.us/rec/share/_jhsItiz4uSpVTWcVzygAfaLmZIAVAKdpT-Qdlf9WIuZ2bLKEZjwwim8JLFpqsn3.0tD1MouRVu3b6PZw
Key Access: e9N*k5^6
(or see Media Gallery)
-
