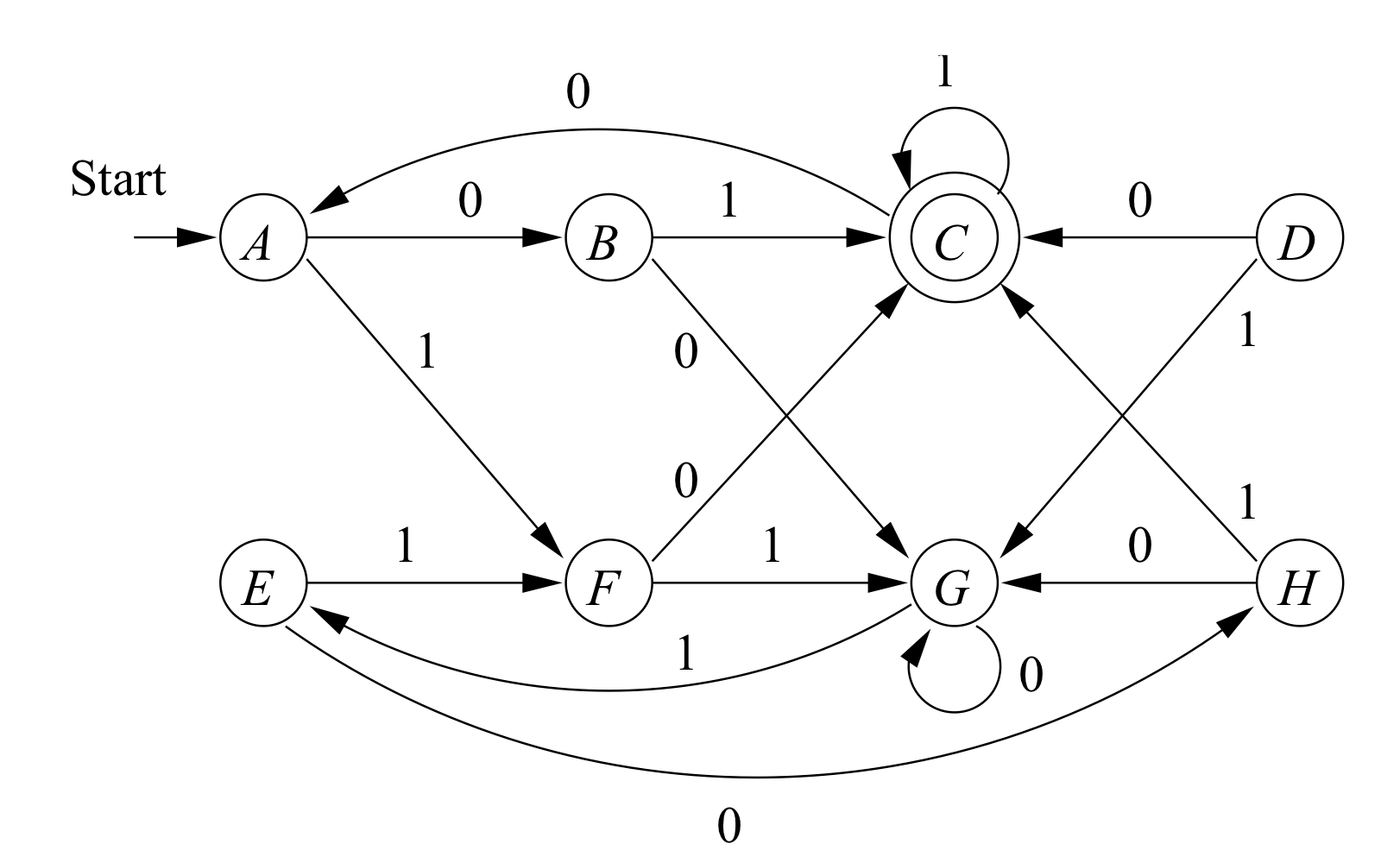
Good evening, I am rereading Chapter 4 on the properties of regular languages and I came across the example concerning Equivalent states:
Let A = (Q,Σ,δ,q0,F) be a DFA, and let p,q ∈ Q.
We define p ≡ q ⇔ ∀ w ∈ Σ* : δ^(p,w) ∈ F if and only if δ^(q,w) ∈ F
Where I assume w refers to a string (following the corollary presented in Chapter 1, page 39 of the first set of slides).
In the example shown below, I do not understand why we are saying that A ≡ E, given that for the string "0" this statement is not satisfied.